Threading and multiprocessing Part 1: How to¶
How to actually DO threading and multiprocessing:
threadingmodulemultiprocessingmodule
Parallel programming can be hard!
If your problem can be solved sequentially, consider the costs and benefits before going parallel.
Parallelization Strategy for Performance¶
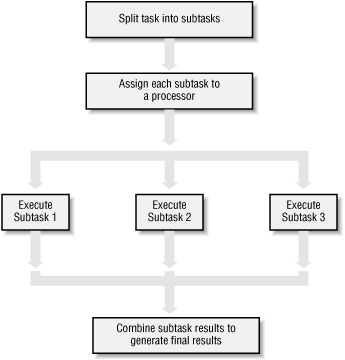
Not every problem is parallelizable.
There is an optimal number of threads for each problem in each environment, so make it tunable.
Working concurrently opens up synchronization issues.
Methods for synchronizing threads:
locks.
queues.
signaling/messaging mechanisms.
The mechanics: how do you use threads and/or processes¶
Python provides the threading and multiprocessing modules to facilitate concurrency.
They have similar APIs – so you can use them in similar ways.
Key points:
There is no Python thread scheduler, it is up to the host OS. Yes, these are “true” threads.
Works well for I/O bound problems, can use literally thousands of threads.
Limit CPU-bound processing to C extensions (that release the GIL).
Do not use for CPU bound problems, will go slower than no threads, especially on multiple cores!!! (see David Beazley’s talk referenced above).
Starting threads is relatively simple, but there are many potential issues.
We already talked about shared data, this can lead to a “race condition”.
May produce slightly different results every run.
May just flake out mysteriously every once in a while.
May run fine when testing, but fail when run on: - a slower system. - a heavily loaded system. - a larger dataset.
Thus you must synchronize threads!
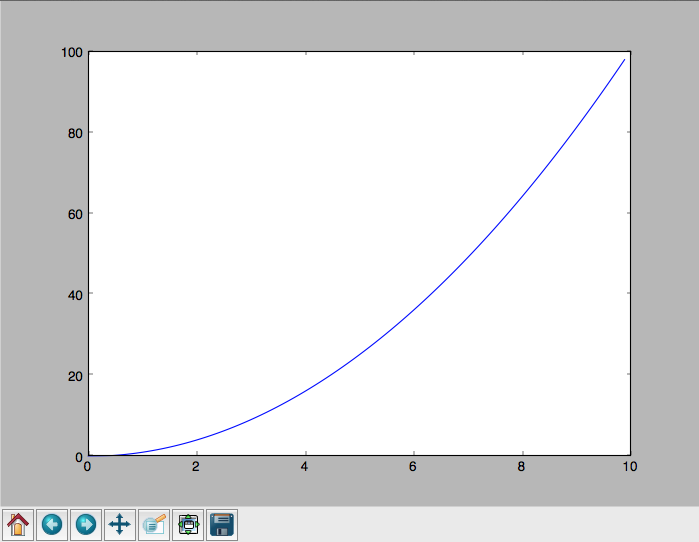
Example: A CPU bound problem¶
Numerically integrate the function \(y =x^2\) from 0 to 10.
http://www.wolframalpha.com/input/?i=x%5E2
Parallel execution example¶
Consider the following code in:
integrate.py
def f(x):
return x**2
def integrate(f, a, b, N):
s = 0
dx = (b-a)/N
for i in xrange(N):
s += f(a+i*dx)
return s * dx
We can do better than this!
Break down the problem into parallelizable chunks, then add the results together: